Mehrstufige Zufallsexperimente
Ein Zufallsexperiment kann aus mehreren Einzelexperimenten zusammengesetzt sein.
Diese können sich gegenseitig beeinflussen oder auch nicht.
Das Baumdiagramm ist dabei das wichtigste Werkzeug, um dies darzustellen.
Bei der Berechnung von Wahrscheinlichkeiten verwendet man die Pfadregel:
- Wahrscheinlichkeiten entlang eines Astes werden multipliziert.
- Die Wahrscheinlichkeiten einzelner „Äste“ werden addiert.
Es soll zweimal gewürfelt werden. Wie groß ist die Wahrscheinlichkeit, im ersten Wurf eine ungerade Zahl und im zweiten Wurf eine Zahl größer als vier zu würfeln?
Lösung mit Hilfe eines Baumdiagramms
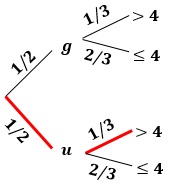Zuerst legt man die Äste für die Ausgänge der ersten Stufe des Zufallsexperiments an und notiert die Wahrscheinlichkeiten.Im Beispiel haben wir Äste für "gerade" g und "ungerade" u jeweils mit einer Wahrscheinlichkeit von 1/2.
An die Endpunkte hängt man nun die Äste für die Ausgänge der zweiten Stufe usw.
Jetzt kann man die Wahrscheinlichkeit entlang des rot markierten Pfades berechnen (denn dieser entspricht dem gesuchten Ereignis).
Es folgt P(E)=1/2·1/3=1/6≈16,7%.
Ergebnis: Die gesuchte Wahrscheinlichkeit (erster Wurf ungerade, zweiter Wurf größer 4) beträgt etwa 16,67%.
Rechenbeispiel 2
Markus und Stefan veranstalten ein kleines Kickerturnier. Markus gewinnt üblicherweise 60% seiner Spiele gegen Stefan. Das Turnier endet wenn einer der Spieler zwei Spiele gewonnen hat. Wie groß ist die Wahrscheinlichkeit, dass Markus gewinnt?
Lösung mit Hilfe eines Baumdiagramms
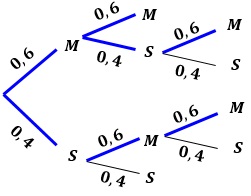
M bedeutet „Markus gewinnt“ und S bedeutet „Stefan gewinnt“.
Die Pfade auf denen Markus das Turnier gewinnt sind blau markiert.
Es sei nun E="Markus gewinnt das Turnier", dann ist E={(M;M), (M;S;M), (S;M;M)}.
Unter Verwendung der Pfadregel ("entlang eines Pfades multiplizieren", "Pfade addieren") erhält man:
P(E) = 0,6·0,6 + 0,6·0,4·0,6 + 0,4·0,6·0,6 = 0,648 ≈ 65%
Ergebnis: Markus gewinnt das Kickerturnier mit einer Wahrscheinlichkeit von etwa 65%.| Downloads |
PowerPoint